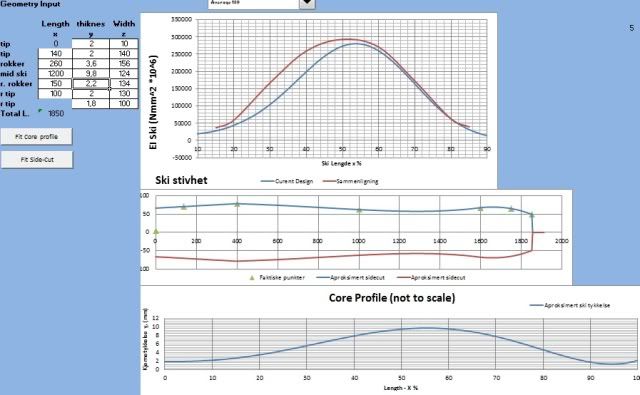
okey, that seems to fit with what i think as well. but i struggled to get the numbers in my spread sheet to match up. i tried to convert some SFI (edit: i mean the N/mm numer read of the graphs at
www.endrehals.no) numbers for the ski i currently use by using this formula:
So for a cantilever beam we have that:
F - Force
y - deflection
0<x<L
y [@x] = (Fx*x^2)*(x-3L)/(6EI) [eq. 1]
this means that:
EI = (F*x^2)*(x-3L)/(6y) [eq. 2]
for Endre's Sfi measurements x = 100, L = 120, F=249 N
So for example [ex.1] 500 N/mm really means 500 N [@x=120]/mm[@x=100]
to be able to convert to EI we need to have 500N[@x=100]/mm[@x=100]
so that we can take 1/( (X N/mm) /249 N) -> mm
to find X we have to find what force F (large) @ x = 100 gives the same deflection as a known force f(smal) @ x = 120, there will be a fixed ratio between these forces. which we can find:
100mm = 5/6 L, 120 = L
we have
y[@ 5/6 L] = -F((5/6)L)^3/12
and
y[@ 5/6 L] = f*((5/6)L)^2*((5/6)L-3L)
if we solve this for F/f -> 1.3
so back to ex.1 this means that y = (249N/1.3)/(500 N/mm), it may seem weird to divide by 1.3, but think like this, the beam would be stiffer if it gave the same deflection with a force @ x = 100 as @ x =120.
Back to eq. 2 it simplyfies to:
EI = (F*x^2)*(x-3L)/(6y)
y = (F/1.3)/( X N/mm), X = ski stiffness
EI = (x^2)*(x-3L)/ ( (1/1.3)/X )
What do you guys think, does this make sense?
Working the numbers, this seems to fit better with my intuition. So now it's just to make a new core profile design.